Talk:Electrical impedance/Archive 2

Archive 1

Archive 2

Archive 3

Very poorly written

I think this site needs a good rewrite. It readly like a bad textbook, i have the feeling much of it is basicaly a copy-edit from some crappy textbooks. Things that say "let v(t) be somecrap" is not only stuffy sounding but useless without the explanation it needs. Not to mention, variables are not explained like they are on every other wikipedia page. Variables need to be explained, I fixed up the first part of the AC steady state part like that - with variables defined in a regular readable way. The other equations should read the same way. Fresheneesz 06:26, 9 December 2005 (UTC)

Holy freaking crap and i just looked at the "see also" section... wtf waaaay too many Fresheneesz 06:29, 9 December 2005 (UTC)

Please don't be a dick, Fresheneesz. More importantly, please don't replace correct statements with obviously incorrect statements such as:

"The general formula for the sinusoidal voltage of a circuit containing resistors, capacitors, and inductors is:"...

In the general case, the amplitude is a function of time. For AC steady state, the amplitude must be constant with time. Further, the objective of this part of the article is to motivate the phasor notation - not to give some general circuit equation. Please try to actually understand the purpose of a section before editing. Alfred Centauri 15:34, 9 December 2005 (UTC)

Sorry, now that I look over it again, after half a year, my statement was pretty freaking wrong. However, I still hold to my dick-like comments above. If this page were well written - I wouldn't have made that mistake.

"objective of this part of the article is to motivate the phasor notation" - I don't think this is the best way to go about this. It can be easily and very understandably said that "Phasor notation is used to simplify circuit analysis by replacing resistances, inductances, and capacitances with a common form - impedances. Impedances can be used almost exactly like resistors, which are much simpler to work with than capacitances and inductances."

I really do hate the "let something be something else" wording. It does indeed remind me of horrible horrible textbooks that hauted my HS and even college career. I mean... why are we letting this something be something else? Is it because its useful perhaps? Or is it arbitrary. In this case it isn't arbitrary, so "letting" something be something else is simply bad wording. Sorry if I'm being a dick. I'm going to change that wording slightly again. Fresheneesz 04:36, 26 April 2006 (UTC)

Simply because you hate some wording because of nightmares from high-school doesn't imply that the wording is inappropriate for an encyclopedic article (in fact, it probably implies th oppposite). Remember, this is not an introductory text book. But heck, if it bothers you that much, change it to something you are more comfortable with. What are you waiting for? Alfred Centauri 02:50, 29 April 2006 (UTC)

Approval? Wait I did change stuff. Fresheneesz 11:24, 28 May 2006 (UTC)

If nothing else, the article could seriously benefit from a layman's explanation. I'd do it, but I don't know how impedence works (on the consumer level) which is what brought me here in the first place. AubreeAnn —Preceding unsigned comment added by 66.30.114.49 (talk) 02:53, 27 April 2008 (UTC)

Sinusoidal basis...

I have removed the following text from the introduction:

"Because these sinusoids comprise a basis (basis means here that we can express any function f(t) as a summation of sine functions using Fourier Series (like in vectors any vector in space can be expressed in terms of i,j,k so i,j,k are called the basis vectors)) over the space of real functions, the impedance of a linear system describes its response to any time-varying signal, not just to a sinusoid."

I have three reasons for this:

(1) The section "Circuits with General Sources" already covers this concept.

(2) This statement doesn't belong, IMHO, in the introductory paragraph.

(3) This statement is not entirely correct. The impedance (as a function of s) of a linear system describes its complex frequency domain voltage response to a time domain unit impulse of current, not a general time-varying signal.

Alfred Centauri 04:21, 21 February 2006 (UTC)

Edits

Please stop inserting the erroneous negative sign in the equation for capacitive impedance. The math, as it stood before your edits, is correct. If you do not see this, then consider the following:

${\frac {1}{j}}=-j\,$

${\frac {1}{j\omega C}}={\frac {-j}{\omega C}}\,$

$X_{C}=\Im (Z_{C})={\frac {-1}{\omega C}}\,$

With the negative sign you inserted, $X_{C}$ becomes positive which is clearly incorrect. Alfred Centauri 00:26, 2 March 2006 (UTC)

Merge Suggestions

Disagree to both merge suggestions. Both articles should instead be candidates for deletion. The author of these two articles has been known to insert unformatted incomprehensible rubbish to the Electromagnetic induction article. Alfred Centauri 21:22, 30 March 2006 (UTC)

Too late, already merged. You do realize that a merge doesn't mean a copy edit - I think my merge smothely incorporates whatever "full electric impedance" may be, and disregards the crappy explanations and definitions that are already better explained in this article. Fresheneesz 05:13, 21 April 2006 (UTC)

circuit symbol

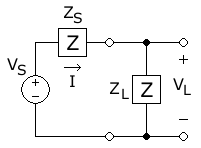
I've seen the circuit symbolization of an impedance element as both a box (like the european way to show a resistor), and I *think* i've seen it also drawn like an american resistance (i can't quite remember). In any case, we should have a picture of how to draw it on this page. Fresheneesz 04:41, 21 April 2006 (UTC)

— Omegatron 15:25, 21 April 2006 (UTC)

Thanks, I'll add that to the intro. Fresheneesz 04:49, 26 April 2006 (UTC)

Also, impedance elements can be shown in the following way. In australia anyway. Element L is the impedance. Nick 04:52, 12 June 2006 (UTC)

Really? That's an inductance everywhere I've seen it. — Omegatron 07:03, 12 June 2006 (UTC)

passive elements only?

I was wondering if impedance only works with passive elements. The only reason I asked is that "passive element" was specified in an article I merged here. Comments? Fresheneesz 05:14, 21 April 2006 (UTC)

Impedance is the ratio of a phasor voltage and a phasor current regardless of whether the voltage and current are associated with a passive or active element or even the same port. Consider the two-port 'z' parameters. [1] Alfred Centauri 14:24, 21 April 2006 (UTC)

See also should be organized

Someone should organize the see also section into subcategories. Fresheneesz 05:18, 21 April 2006 (UTC)

AC steady state

The information under the header "AC steady state" seems very far disconnected with impedances. This article is on impedances, not on phasor notation. Obviously they can be interrlated, but that section is not a good starter. We should start on what impedances are - not what voltage is. Fresheneesz 04:57, 26 April 2006 (UTC)

I disagree - AC steady state is crucial to the development of the impedance concept. If you don't see this, then you don't quite understand impedance. Let's say that an RC circuit is driven by a sinusoidal source with frequency f but the circuit is not in steady state. What is the impedance of the capacitor?

And, although this article is not on phasor notation, what does an impedance multiply? A time domain current? A frequency domain current? Or, is it a phasor current? Is the result a time domain voltage, frequency domain voltage, or a phasor voltage? Alfred Centauri 21:53, 26 April 2006 (UTC)

I may not fully understand impedances, but I know how to use them. Thats part of my point, people comming to this page may not want to know the derivation for impedances - just how to use them. So starting the page off with intricacies isn't best.

"what does an impedance multiply" - what do you mean by that, I don't understand that question. 68.6.112.70 03:32, 28 April 2006 (UTC)

I would fully agree with you - if this article were part of a textbook. If people want to learn how to use impedances, then they should try Wikibooks, don't you think?

An impedance multiplies a phasor current and the result is a phasor voltage. Thus, it seems reasonable (to me) to believe that in order to define an impedance, which is the ratio of voltage and current phasors, requires an introduction to phasors. Can you describe a better way? If you were re-write this article, how would you define impedance and then give examples of how an impedance is used without introducing phasors first? Alfred Centauri 02:38, 29 April 2006 (UTC)

"If people want to learn how to use impedances, then they should try Wikibooks, don't you think?" - yes and no. If they want a step by step in depth discussion of how to use impedances, then wikibooks would be the place. But if they want a concise overview of how people use impedances, then I think wikipedia is a perfect spot for that.

And... don't you think that perhaps an introduction to phasors belongs in wikibooks instead of here. Or perhaps just on the page on phasors. This is one thing I would do if I were to rewrite this page - get rid of the intro to phasors, and instead link the word phasors to the article on phasors (which I think is probably done). People comming here want to know about impedances, not phasors - but if they do want to learn both, they can visit both pages. Fresheneesz 22:01, 15 May 2006 (UTC)

non-phasor impedances

I've recently learned that "impedance" is not one thing. What I mean is that the term impedance is used in more than just phasor circuit analysis. For example, in Laplace transformations, circuit elements can be transformed into impedances in the s-domain. This article (as far as I can tell) focuses only on phasor impedances, and disregards the existance of s-Domain impedances. They are very interrlated concepts, and s-domain impedances should have a place on this page. Fresheneesz 04:59, 26 April 2006 (UTC)

Actually, impedance is just one thing - it is the ratio of the voltage to the current when the circuit excitation is of the form:

$Ae^{s_{0}t}\,$

See the discussion under 'Rv of last edit by Wigner'. It is precisely because the complex exponential is the eigenfunction of the derivative operation that, for a capacitor or an inductor driven by a complex exponential source, the ratio of the time domain voltage to current is the same as the ratio of the frequency domain voltage to current. Recall that, for a resistor, the resistance R is the ratio of the voltage to current in both the time domain and the frequency domain for any excitation.

Now, it is my opinion that the the ratio of the frequency domain voltage to current for an arbitrary excitation is not technically an impedance. On a couple of occasions, editors have added verbage to this effect and I have removed it. The reason is that for an arbitrary excitation we still have:

$V(s)=Z(s)I(s)\,$

but, in the time domain, we now have:

$v(t)=z(t)*i(t)\,$

where * is convolution.

What is this z(t)? Consider a capacitor driven by a constant current source. The ratio of the time domain voltage to current is a function of time:

${\frac {v_{C}(t)}{i_{C}(t)}}={\frac {t}{C}}$

Would you call this an impedance? Alfred Centauri 14:03, 26 April 2006 (UTC)

I guess? Not quite sure.

"it is the ratio of the voltage to the current when the circuit excitation is of the form...." - I'm pretty sure that Laplace impedances don't require the function to be sinusoidal at all - especially not in that specific form. This is why they're useful over phasors.

"For example, what is the impedance of a capacitor if the voltage across the capacitor is:

$v_{C}(t)=cos(2\pi f_{1}t)+sin(2\pi f_{2}t)\,$"

I actually used Laplace transformations to derive the impedance of the capacitor in that case:

$Z_{C}(t)={\frac {1}{2\pi f_{2}}}+{\frac {sin(2\pi f_{2}t)}{4\pi f_{1}C}}-{\frac {cos(2\pi f_{1}t)}{2\pi f_{2}}}\$

where C is the capacitance.

"my opinion that ... is not technically an impedance" - I think it technically *is* an impedance, but perhaps you'd rather not think of it as such. Laplace impedances are still voltage over current - but are more general than phasor impedances. Fresheneesz 03:05, 27 April 2006 (UTC)

(1) Impedance is not a function of the instantaneous values of the voltage and current. Don't take my word for it - look it up. Point me to a reference that says otherwise.

(2) IMHO, you are confusing transfer functions with impedances. The ratio of Laplace (and Fourier) voltages and currents are transfer functions.

(3) What you derived from the Laplace transform is not an impedance and further, it is clearly not the ratio of the time domain voltage and current associated with the capacitor which is given by:

${\frac {1}{2\pi C}}{\frac {cos(2\pi f_{1}t)+sin(2\pi f_{2}t)}{f_{2}cos(2\pi f_{2}t)-f_{1}sin(2\pi f_{1}t)}}$

The Laplace transform of cos(t) and sin(t) actually assume that the time signals are u(t)cos(t) and u(t)sin(t) respectively. That is, the sinusoidal sources 'turn on' at t=0. If you use the Fourier transform (and its inverse), you should get the same answer as I get. In any case, these time functions are not impedances. Once again, if you can find anything in the literature that says otherwise, I would be very interested to see it. Alfred Centauri 04:05, 27 April 2006 (UTC)

I did probably confuse transfer function for impedance in my largish function, fair enough. But in the s-domain, the laplace impedances *are* V(s)/I(s). They work like normal impedances, and are defined for more functions than sinusoidal ones. Fresheneesz 07:23, 27 April 2006 (UTC)

"They work like normal impedances, and are defined for more functions than sinusoidal ones" Sigh. I think that you are not seeing the deep connection between phasors and the Laplace (or Fourier) domain. Maybe you'll see soon that what you've said here (and have added to the Laplace transform page) is nonsense. Maybe this will help - think of what the difference might be between an impedance function and an impedance proper. What is the difference between 1/Cs and 1/Cs_o? This is subtle so take your time. Alfred Centauri 13:55, 27 April 2006 (UTC)

Something else to consider. In words, what does the ratio V(s)/I(s) represent? What if i(t) is the unit impulse? Then I(s) = 1 so that the ratio V(s)/I(s) = V(s). Now we see that this ratio is simply the Laplace transform of the voltage response to the unit impulse of current. In other words, a transfer function. Alfred Centauri 14:15, 27 April 2006 (UTC)

I've been taught that the connection between phasors and the Laplace domain is that phasors are a subset of the Laplace domain - where $s=j\omega$. Replacing the "s" in Laplace impedances with "$j\omega$" gives the phasor impedance. Is this wrong? Fresheneesz 02:08, 28 April 2006 (UTC)

A phasor is the complex amplitude associated with a time function of the form:

$Ae^{s_{0}t}\,$

In physical circuits, we don't find time functions of this form since this time function is complex valued. However, we can find time functions of the form:

$\Re {(Ae^{s_{0}t})}\,$

For AC (sinusoidal) circuit analysis, we assume that the real part of s_0 is zero so that the voltages and currents are of the form:

$\Re {(Ae^{j\omega _{0}t})}\,$

To do the analysis, we pretend that the time functions are of the form:

$Ae^{j\omega _{0}t}\,$

and then take the real part of the solution at the end.

But, this doesn't diminish the fact that a phasor is the complex amplitude of a complex exponential function of time. How does this all tie in with the s-domain?

First, recognize that the ratio of the s-domain voltage to current associated with a circuit element is, by definition, the Laplace transform of the time domain voltage response to a time domain unit impulse of current. To see this for a capacitor, take the inverse Laplace transform of 1/Cs:

${\frac {1}{C}}u(t)\Leftrightarrow {\frac {1}{Cs}}$

That is, a unit impulse of current through a capacitor produces a step of voltage scaled by 1/C.

Such a function in the s-domain is called a transfer function. Since this function has units of ohms, it is appropriate to call it an impedance transfer function. What must be understood is that this function is not an impedance proper. Now, let us evaluate this impedance transfer function for some particular value of s which we will denote as s_0. What does this quantity represent? It is straightforward to show that this quantity is equal to the ratio of the complex amplitudes of the time domain voltage and current functions associated with a capacitor when they are of the form:

$Ae^{s_{0}t}\,$

Try to show this mathematically - you will need to use the delta function in the s-domain - delta(s - s_0) - as the s-domain current in order to select the value 1/Cs_0 from the function 1/Cs. So, 1/Cs_0 is equal to the ratio of the voltage and current phasors when s = s_0. This defines the impedance of the capacitor when s = s_0.

So, can phasors be used for more general sources? The answer is, of course, yes if the Laplace transform of the source function exists. If we calculate the s-domain voltage across a capacitor for some general s-domain current, we must take the inverse Laplace transform in order to find the time domain voltage function, right? But, if you consider what the process of taking the inverse transform is, you see that it is simply the 'summing up' of complex exponential time functions (with different values of s) scaled by the impedance of the capacitor at that particular value of s. See the section in the article entitled "Circuits with general sources". So you see, phasors are built-in to the inverse Laplace transform. Alfred Centauri 03:54, 28 April 2006 (UTC)

On last thing, replacing s with jomega, in the case of the bilateral Laplace transform, simply gives the Fourier transform of the impulse response (or, in the case of unilateral transform, don't forget the implicit multiplication by u(t)). In other words, you still end up with an impedance transfer function which, when evaluated at some value of omega, gives the ratio the phasors associated with:

$Ae^{j\omega _{0}t}\,$

Alfred Centauri 04:21, 28 April 2006 (UTC)

One small point I have: Impedance depends on the input wavefunction, as is shown by its dependance on ω. Thus by saying all impedances are phasor impedances, you constrain those impedances to be only sinusoidal, and lose the generality of arbitrary input waveforms. In short, the impedance depends on s, whether or not s = jω Fresheneesz 21:54, 15 May 2006 (UTC)

part 2 of discussion

Fresheneesz, after all I went through above, your response is like you didn't read or understand any of it! OK then, let's try a different approach using your phrasology. Please give me an example of an input waveform that cannot be handled by phasor impedances. Alfred Centauri 22:23, 15 May 2006 (UTC)

Alright, how bout the unit impulse. (btw, thanks for being patient). Fresheneesz 07:53, 16 May 2006 (UTC)

Alright then, the unit impulse. What impedance does a capacitor present to a unit impulse of current? Alfred Centauri 13:26, 16 May 2006 (UTC)

Well... its s-domain impedance is 1/(sC). I don't know what else to say to that. Fresheneesz 08:40, 20 May 2006 (UTC)

You should at least justify you claim above that the unit impulse cannot be handled by what you call phasor impedances. Also, please justify your claim above that the impedance depends on the input waveform. After all, what you call the s-domain impedance in your answer above does not depend on the input waveform does it? You could describe what is the significance of 's' in the answer you gave above. What does it mean? How does one use it? Why is this 's' somehow better than jω for handling the unit impulse as an input waveform? Alfred Centauri 14:15, 21 May 2006 (UTC)

Well, I wouldn't think that i'd have to explain these things to you... but... phasors require a constant frequency, which doesn't work for any arbitary wavefunction. And setting omega = to 0 after time 0 gives you an impedance of infinity, which is obviously incorrect except at t=∞. And impedances depend on the input waveform because capacitors and inductors are reactive elements. At 0 frequency (for all time), a capacitor has infinite impedance - and for infinite frequency (for all time), a capacitor has 0 impedance.

And the impedance for the capacitor does depend on the input, however it doesn't depend on the s-domain version of the input (which makes s-domain impedance more useful). As for the significance of s, I'm not an expert in laplace tranforms, but s is a parameter that can be related to the frequency of the input. One can substitute jω for s and find the frequency response. The s-domain is "better" than phasors for handling the unit impulse, because phasors require a constant frequency and laplace transformations don't. Fresheneesz 19:51, 21 May 2006 (UTC)

I wanted you to explain it to me so I could better understand what is it you don't understand. What you've 'explained' to me above is incorrect and demonstrates that you don't understand impedance or the relationship between phasors and the s-domain or even the relationship between the s-domain and the time domain. I actually thought I had expained some of this rather well in my lengthy post above. However, either I failed to do so or you didn't bother to try to understand what I wrote. I'll close by individually addressing some of the things you said above:

"phasors require a constant frequency, which doesn't work for any arbitary wavefunction." Yes, a phasor is associated with a particular frequency but that in no way implies that phasors cannot be used for arbitrary waveforms.

"And setting omega = to 0 after time 0 gives you an impedance of infinity, which is obviously incorrect except at t=&infin". This sentence is not even wrong - it is meaningless.

"And the impedance for the capacitor does depend on the input, however it doesn't depend on the s-domain version of the input (which makes s-domain impedance more useful)." Again, not even wrong. At best, this statement can be described as confused.

"As for the significance of s, I'm not an expert in laplace tranforms, but s is a parameter that can be related to the frequency of the input." How can this be? As you've already correctly stated, 1/sC is independent of the input signal.

"One can substitute jω for s and find the frequency response." This is the closest you came to demonstrating some understanding of this subject. It's not quite a correct statement but it's not far off.

"The s-domain is "better" than phasors for handling the unit impulse, because phasors require a constant frequency and laplace transformations don't." Yeah, you've said this before but no matter how many times you say it, the fact that it is wrong is not going to change.

Now that I understand the depth of you confusion, I'll be reviewing your edits much more closely. Alfred Centauri 21:13, 21 May 2006 (UTC)

Hmm. Instead of saying my points are wrong, most of those points say that i'm "close" or "not far off". As I've said before, i'm not an expert. Not to give you fodder for more ridicule, but in fact, I'm a student. And I know for 100% certainty that s-domain impedances are *taught as impedances*.

Anyways, tell me how phasors can be used for arbitrary wavefunctions, if they require a wavefunction with a constant frequency. Surely there are many many waveforms that do not have a constant frequency.

"This sentence is not even wrong - it is meaningless" - What I meant is that, using phasor impedances, a DC input voltage sees a capacitor as an open circuit - infinite resistance/impedance. Just because you don't understand what I write, doesn't mean its meaningless.

"As you've already correctly stated, 1/sC is independent of the input signal" - 1/sC is independant of the s-domain input signal. However since s depends on the time-domain input, 1/sC depends on the time-domain input. What I mean by "the impedance varies with the input" is that the resistance shown by an impedance element depends on the input signal (and of course the element itself).

You say my thoughts are wrong, yet you give little to no justification for those statements. Could I respectfully ask that you cut to the chase? Fresheneesz 00:12, 22 May 2006 (UTC)

That the s-domain transfer impedance for a capacitor or inductor is taught as an impedance I do not deny. Often, we in the EE world use technical words imprecisely but this often leads to the kind of confusion you have been led to. But tell me, did you honestly attempt to digest the material I posted earlier? I ask this because you have requested that I 'cut to the chase' but I wonder if there is any reason to try since you don't appear to have absorbed any of the earlier information I posted. To work out what I perceive to be your misconceptions will require that you think carefully about what I say because much of this is subtle.

You ask me to tell you how phasors can be used with arbitrary input functions. Yet, I have already explained that in the article section 'General sources'. I'm sure you are aware that virtually all the signals of interest in EE have a Fourier series or Fourier integral representation. What comes out of the analysis integral at a particular frequency is a constant complex number. What is this number? It is none other than the phasor representation of that frequency component contained in the signal. In other words, the Fourier transform of a signal is precisely the set of phasors associated with the spectral components of the signal. Do you see? If we take the Fourier transform of the unit impulse current signal and multiply that by the impedance transfer function for the capacitor (1/jωC), we have multiplied each phasor component of the input signal by the impedance of the capacitor at the frequency of that component. To get the time domain voltage response, we take the inverse Fourier transform, right? But consider what this inverse transform is. We take the phasor voltage at a particular frequency and multiply it by a sinusoidal time function at that frequency and we do that for every frequency and then 'add' all of them up at a particular value of time. Do you get the picture now?

What is the relationship between the Laplace transform and the Fourier transform? To answer that, let's first assume that our time-domain function is equal to zero for t<0. Then, it is easy to see that if F(jω) is the Fourier transform of f(t), then F(s) [where s = σ + jω] is the Fourier transform of f(t)exp(σt). Clearly, for the Laplace transform to exist, we must have σ < 0 - a decaying exponential. Do you see the connection? What is the implication of this?

BTW, your sentence about infinite impedance at DC is meaningless and it's not because I don't understand what you were 'trying' to say. It is because you have put together phrases that don't make any sense in the context of impedance. Also, connect a DC current source to a capacitor and tell me if it really appears to be an open circuit.

You said "1/sC is independant of the s-domain input signal. However since s depends on the time-domain input, 1/sC depends on the time-domain input." On the contrary, s does not depend on the time-domain input signal. Maybe you are trying to say something else here but I can assure you that s does not depend on the time-domain input signal.

I would never ridicule you for any reason other than a stubborn refusal to try to understand what I have explained here and in my earlier lengthy post. BTW, I am a student also so you can't use that excuse with me ;<) Alfred Centauri 01:52, 22 May 2006 (UTC)

I did honestly try to understand what you wrote above. But lets recap what exactly we're arguing:

Basically, the bottom line is that you're saying 1/jωC is an impedance, but 1/sC is not. Not only that, s doesn't depend on the input signal. I know for a fact that that second assertation is not true. For example, for a sinusoidal input (where phasors apply as well), s = jω. ω is derived from the input waveform, therefore s depends on the input waveform.

I do see the connection between the fourier transform and the laplace tranform. And I realize that all real inputs are a superposition of sinusoidals. So ok, I was wrong about phasors not working for general waves. I'll concede there. Fresheneesz 18:29, 26 May 2006 (UTC)

"Basically, the bottom line is that you're saying 1/jωC is an impedance, but 1/sC is not.". Sorry, but no, that is not what I'm saying. Here's a question for you. What is the difference in the meaning of the variable s used in the following two equations?

$v_{C}(t)/i_{C}(t)={\frac {1}{sC}}$

$V_{c}(s)/I_{c}(s)={\frac {1}{sC}}$

I believe that if you know and understand the answer to that question, you should understand what I'm trying to say regarding impedance.

"Not only that, s doesn't depend on the input signal. I know for a fact that that second assertation is not true." s does not depend on the input signal. s is the variable of the kernel of the Laplace integral transform. It is not possible for that variable to depend on the function being transformed. The only thing I can think of that you may be trying to say here is that the function of s that comes out of the Laplace transform depends on the time-domain signal. If this is what you mean, then you have made a correct but trivial statement. After all, in the theory of Laplace transforms, there is a one-to-one correspondence between the frequency and time-domain representations of a signal. However, if this is not what your are trying to say then please give me an example where the Laplace variable s depends on the time-domain signal being Laplace transformed. Alfred Centauri 22:15, 26 May 2006 (UTC)

To answer your first question, the second equation is a regular laplace imedance. I'm no too sure about the actual meaning of s in the s domain - my first thought was that it is some sort of constant that depends on the input. For the first equation to be true of a capacitor, s must be a function of time.

"give me an example where the Laplace variable s depends on the time-domain signal" - I already gave you an example, and you ignored it. I wrote:

"For example, for a sinusoidal input (where phasors apply as well), s = jω. ω is derived from the input waveform, therefore s depends on the input waveform." Fresheneesz 01:29, 28 May 2006 (UTC)

That you don't know the actual meaning of s in the s domain and that you believe that s must a function of time in the first equation explains helps me understand why you believe that a sinusoidal signal demonstrates that s depends on the input waveform.

part 3

The simple fact is that s is a complex parameter that is not a function of time nor does it depend on the input function. You will hopefully see all this when you understand what the actual meaning of s is. Good luck in your studies. Alfred Centauri 02:23, 28 May 2006 (UTC)

Thanks for the luck, but you ignored my example for the second time. Am I wrong that s depends on ω for a sinusoidal input? Fresheneesz 11:20, 28 May 2006 (UTC)

Here's what I asked for: "...please give me an example where the Laplace variable s depends on the time-domain signal being Laplace transformed." You have confirmed twice that the example you wish to give is a 'sinusoidal input'. Alright then, let the time domain capacitor current be sinusoidal:

$i_{C}(t)=A\cos {\omega t}+B\sin {\omega t}\,$

where t is an independent real variable and ω is a given real parameter

The Laplace transform of this sinusoidal input current is then given by:

$I_{c}(s)=A{\frac {s}{s^{2}+\omega ^{2}}}+B{\frac {\omega }{s^{2}+\omega ^{2}}}$

where s is an independent complex variable.

Now, will you please explain to me why you insist that the independent complex variable s in the later equation above depends in any way on the former equation or for that matter, on ω? Alfred Centauri 12:35, 28 May 2006 (UTC)

Well, I don't understand exactly why this is, but replacing s with j ω does give you regular phasors. This is correct, right? Could you explain to me why replacing s with j ω is done, because I don't understand it fully. However, my argument hinges on the fact that ω is part of the input waveform, and if s depends on ω then it also depends on the input. Fresheneesz 20:02, 28 May 2006 (UTC)

Recall an earlier comment where I wrote...

"What is the difference in the meaning of the variable s used in the following two equations?

$v_{C}(t)/i_{C}(t)={\frac {1}{sC}}$

$V_{c}(s)/I_{c}(s)={\frac {1}{sC}}$

I believe that if you know and understand the answer to that question, you should understand what I'm trying to say regarding impedance."

The answer is that in the first equation, s is a parameter while in the second equation, s is the independent variable. Your argument is based on not drawing a distinction between the two. The fact that the same notation is used here isn't helping you see the distinction. That's why I usually distinguish between the two by using a subscript 0 for the parameter so my previous equations would now look like:

$v_{C}(t)/i_{C}(t)={\frac {1}{s_{0}C}}$

$V_{c}(s)/I_{c}(s)={\frac {1}{sC}}$

and

$i_{C}(t)=A\cos {\omega _{0}t}+B\sin {\omega _{0}t}\,$

where t is an independent real variable and $\omega _{0}$ is a given real parameter

The Laplace transform of this sinusoidal input current is then given by:

$I_{c}(s)=A{\frac {s}{s^{2}+\omega _{0}^{2}}}+B{\frac {\omega _{0}}{s^{2}+\omega _{0}^{2}}}$

where s is an independent complex variable.

Now, if you do the replacement s = jω, you get the following:

$I_{c}(j\omega )=A{\frac {j\omega }{-\omega ^{2}+\omega _{0}^{2}}}+B{\frac {\omega _{0}}{-\omega ^{2}+\omega _{0}^{2}}}$

See the difference? In the last equation, ω is the independent variable while $\omega _{0}$ is a number - a parameter. The Bode plot of this current would have log(ω) on the horizontal axis while $\omega _{0}$ would appear as a point on this axis. Get the picture? Alfred Centauri 22:03, 28 May 2006 (UTC)

Update: to address your question of why replace s with $j\omega$: recall that s is a complex variable with a real part and an imaginary part. This is often written mathematically as:

$s=\sigma +j\omega \,$

So, σ is the real part of s and ω is the imaginary part of s. If we choose to set σ to zero, the (bi-lateral) Laplace transform is identical to the Fourier transform. However, in the case of $s_{0}$ (a parameter in a time domain equation), if we set $\sigma _{0}$ equal to zero, we get the familiar 'phasor' form, e.g.,

${\frac {1}{s_{0}C}}={\frac {1}{j\omega _{0}C}}when\sigma _{0}=0$

Alfred Centauri 01:26, 29 May 2006 (UTC)

Ok I sorta think I see what you've been saying. Does part of it involve that the input waveform depends on ω and so does s, but s doesn't depend on the input?

Also, to bring this conversation back to its original point, I think that there should be at least a small note on the name "laplace impedances" and what that means as opposed to the impedances on this page. What do you think? Fresheneesz 19:45, 29 May 2006 (UTC)

Let me try again. You are confusing the ω that is the imaginary part of s with the frequency parameter of the time domain signal. These are not the same variables! Maybe this will help you to 'see' this:

$v(t)=V_{p}cos(\alpha t)\,$

$V(s)=V_{p}{\frac {s}{s^{2}+\alpha ^{2}}}$

$V(j\omega )=V(s)|_{\sigma =0}=V_{p}{\frac {j\omega }{-\omega ^{2}+\alpha ^{2}}}$

s and ω do not depend on the input v(t) in any way whatsoever. You can specify α to be any real number and I can specify σ & ω to be any real numbers without regard to your choice of α. The only thing that depends on both of our selections is the value of V(s) for a given α, σ, & ω. Alfred Centauri 13:11, 30 May 2006 (UTC)

Sorry guys to interrupt. I've finished UK A-Levels (lol) including Physics, and have heard of impedance before. I believe it has something to do with resistance, and from what I've heard/read so far, it has something to do with resistance in circuits in which alternating current passes. However, this page is very confusing. I checked Wikibooks and found nothing on this subject. Could someone possibly describe qualitatively what impedance is, and whether I'm right in saying how it is related to resistance (above)? I am interested in what it is.

In addition, I think I found a website a while ago which explained impedance simply. However, (typical of me) I forgot what it said and forgot what the address is. If I find it, can I put a link to it in the External Links section of the main article? Thanks in advance. --FSHero 10:10, 31 July 2006 (UTC)

Thankyou, thankyou! I too turned to this page to re-inform myself of my understanding of the term (my EE courses were 35 years ago). This article is apparently addressed to people who can argue over it, not to those seeking understanding. --Kcrossle 15:23, 31 August 2006 (UTC)

lol! Unfortunate... FSHero 14:55, 18 September 2006 (UTC)

Needs a phasor Diagram

This article needs a phasor diagram, to show geometrically what the impendance is. RZ heretic 00:55, 1 November 2006 (UTC)

Shockingly bad

With all respects to the editors who are certainly trying hard, there is much in this article which is so poorly stated and imprecise that it is misleading. (By the way, this seems to be true not just of this article but also of others in the EE domain). I would not send a student to this site to use it as a reference because of the errors. Every undergraduate electrical engineering textbook treats this subject with better explanations and without the errors. This article is full of redundancies and contradictions, its too hard to go through this line by line to correct it all. Please, editors, look at an EE circuits textbook for the appropriate definitions, try to not dumb down the concepts so casually and *please* leave out the bizarre generalizations.

I do agree that this article badly needs rewriting, which I plan to do shortly. Moreover, the last edits are really bad. There are not such things as "full", "effective" or "reactive" impedances. There is just "impedance" which is a complex number with a real part and an imaginary part. LPFR 13:26, 5 November 2006 (UTC)

As a casual reader, I also groaned I saw those silly phrases. My suggestion to the editor LPFR above is to simply blow it all away and start over, if they will let you.

You clearly are ignorant of how Wikipedia works. First, if you see something that is wrong then fix it - 'armchair' editors are not welcome here. Second, blowing an article away is simply bad form here and will almost certainly be reverted. Third, and most importantly, are you really so naive as to think that a complete rewrite of this article will fix it? Don't you understand that every Tom, Dick, and Harry that has just skimmed a copy of some generic "Introduction to Electronics" book will edit the rewritten article until it looks pretty much the same as it does now? Are you prepared to monitor the "Electrical Impedance" article from now on and revert any edits that don't meet your standards? If so, wouldn't that make you part of the 'they' you derisively referred to? Alfred Centauri 22:44, 6 November 2006 (UTC)

I'm afraid that User:Alfred Centauri is right. I stop any further collaboration with WP. It is worthless to write anything if any low-level knowledge and high-ego person will "correct" your writings. I think that WP is doomed to represent the "mean-street-knowledge" level. I was puzzled reading the scientific level of serious wikipedians (as project members). You seldom or never found University teachers or retired academic members. The best you found are engineers or thesis students. Of course, you do not need to be old or have academic titles to know things, but it helps. I now understand why there are so few university teachers and experienced people. Last edits in this article washed out my last wishes to be useful. -- LPFR 09:27, 17 November 2006 (UTC)

Removed sketch

I removed this sketch, under the heading "Four Quadrant Operation":

File:Elimp2.jpg

--Heron 20:56, 8 February 2007 (UTC)

Possible changes

This article contains a lot of useful information, however I feel that anyone who is not already reasonably familiar with the concept of impedance is likely to leave non the wiser.

I am a grad student in experimental physics and recently wrote a short paper on impedance for the benefit of undergrad project students in our lab and thought it might be nice to put a version of it online.

I have created an initial outline that you can find here.

I realise that a lot of people have put a lot of work into this article over the years and I don't want to step on peoples toes; my main concern is to make clear from the beginning how impedance differs from resistance, particularly the inclusion of the voltage-current phase relationship.

I would appreciate comments from any and all interested parties on my talk page.

--DJIndica 23:51, 26 May 2007 (UTC)

See my comments above in the section titled "Shockingly Bad". To summarize, feel free to make wholesale changes if you like; be bold. I did the same thing a couple of years ago and it is time for this article to be 'reset' again. Just keep in mind that this article is subject to lots of well-meaning but ill-informed edits. Alfred Centauri 01:54, 27 May 2007 (UTC)

The edit on DJIndica's page looks like a pretty big improvement in understandability. I would guess quite a bit of information is left out of that subpage that's in the current one, but the new edit looks good enough to replace the current one, as long as the left out information is considered. Fresheneesz 19:23, 27 May 2007 (UTC)

I have made the changes to the article, I have removed quite a lot; I hope people will consider carefully before reinstating sections. Where I have removed things it is because I do not think it helps explain the concept of impedance, I have generally included links to more in depth articles on the removed topics.

Comments welcome!--DJIndica 03:41, 3 June 2007 (UTC)

Resistance and Ohm's Law

Ohm's law could be viewed as the definition of a fixed resistor. In that case, impedance "generalizes" Ohm's law. If Ohm's law is a behavioral relationship then it says things like v(t)/i(t) = R for any ideal voltage or current source, not just sinusoidal AC. Because it is called a "law," I have always thought Ohm's law referred to a behavioural relationship, otherwise it would be called Ohm's definition. But maybe I am confused. gaussmarkov 08:54, 26 June 2007 (PDT)

IMHO, Ohm's law is a law in the context of physics. However, in the context of (ideal) circuit theory, a resistor circuit element is defined as that circuit element where v(t) = R i(t). That is, Ohm's law defines the ideal resistor circuit element in the context of circuit theory. Alfred Centauri 16:46, 26 June 2007 (UTC)

That makes sense. Thank you for responding. Perhaps the article should have some sort of statement that it is about ideal circuit theory? I hope it's alright if I press my question a little: Ohm's law as a definition of the ideal fixed resistor places no restrictions on v(t) or i(t) other than their proportionality. They do not have to be proportional sinusoidal AC. As I understand this article, it says that the definition of impedance requires sinusoidal AC. How can impedance be a generalization if it makes an additional restriction? All the best, gaussmarkov 19:58, 26 June 2007 (UTC)

Yes, I see your point and it is a good one. Consider the following: if the source in an ideal circuit has the form of a complex exponential and the circuit is in steady state, the voltage and current relationship for any resistor, inductor, or capacitor in the circuit has the form of Ohm's law: v(t) = Z i(t). In such a circuit, the inductor and capacitor have an imaginary valued Z while the resistor has a real Z. This is the generalization referred to in the article - the application of an Ohm's law like relationship to inductors and capacitors when certain conditions hold. What do you suggest for a different word or phrase to use here that would improve the accuracy of the article? Alfred Centauri 23:41, 26 June 2007 (UTC)

Great. I tried to be bold and took your question as an invitation to write the wording. I also offered a slight re-organization of the introductory paragraph. I am hopeful, of course, that this is helpful. gaussmarkov 06:04, 27 June 2007 (UTC)

I'm not convinced that impedance is analogous to resistance. The concept of impedance is clearly some type of extension of the concept of resistance since resistance is a component (the real part) of impedance. Please reconsider your edit. Alfred Centauri 21:56, 27 June 2007 (UTC)

For lack of any objection, I've changed 'analagous' to 'an extension of'. Alfred Centauri 02:15, 30 June 2007 (UTC)

I like the use of extends to rather than analog of, I have used the same language in the Ohm's law section. I'm not happy with "Often, impedance is represented formally as a complex quantity"; for the general case impedance is a complex quantity, the article makes this clear by discussing its real and imaginary parts (and magnitude and phase). This was changed very recently by gaussmarkov, I would like to change it back but would be interested to hear any opposing arguments.--DJIndica 15:14, 1 July 2007 (UTC)

The change to extends to is fine with me. I think it is a good choice.

I do not think that impedance is a complex quantity. I think it is merely a two-dimensional concept. Commonly, we refer to its magnitude and its phase. These are not inherently related to complex representations, though that is formally (or algebraically) convenient. Alternatively, we refer to its resistive and reactive dimensions. Again, there is no necessary connection with the complex plane. To make this point another way, all of the derivations can be carried out without complex algebra.

I see that there is also some confusion about these matters remaining in the article. In section titled Complex voltage and current, someone states

we must bear in mind that these are real quantities and take only the real part at the end of a calculation.

Actually, we typically want the magnitude and the phase, neither of which is the real part. gaussmarkov 23:01, 5 September 2007 (UTC)

"I do not think that impedance is a complex quantity". Impedance is a complex quantity by definition as it is the ratio of the voltage and current phasors regardless of your argument to the contrary. All that matters here are authoritative references of which there are plenty that dispute your assertion. BTW, taking the real part of the complex exponential form of the voltages and currents does give the magnitude and phase as part of the real time dependent function which is, in the end, precisely the form of the actual voltages and currents. Perhaps you were thinking that the section implied taking the real part of the phasors instead? Alfred Centauri 00:48, 6 September 2007 (UTC)

Hmm. We may not be able to get the authorities to agree on the definition of impedance. What do you consider to be an authority? I have not seen any citations to authorities here. The references at the end of the article surely don't qualify. I will try to find time to go to the library tomorrow.

Perhaps it would be helpful to distinguish between impedance and complex impedance, as many authors do? You would then be referring to the latter. Impedance without modifiers is variously defined, sometimes as complex, sometimes as the ratio of the amplitudes of sinusoidal voltage and current, and sometimes as the ratio of appropriately phase-shifted voltage and current. In the last two cases, impedance is only the magnitude of complex impedance. But I think that I have also seen it defined as a vector (not specifically complex) so that phase is included. There is plenty of physics course material online that bears out what I am saying. See for example, http://www.physclips.unsw.edu.au/jw/AC.html#impedance. Or the external link at the end of the article, which refers to the complex impedance method.

If impedance is indeed a complex quantity, then we will have to change its units. The ohm is not a complex unit of measure. Stating, as the article does, that the SI unit of impedance is the ohm suggests that impedance refers only to the magnitude as just described.

On the second point, my answer to your question is yes, I was thinking of the phasors because that is what the text is discussing. Let's take the text apart. The complete thought is

In order to simplify calculations, the voltage and current are commonly represented as complex quantities denoted as $\scriptstyle {\tilde {V}}$ and $\scriptstyle {\tilde {I}}$; we must bear in mind that these are real quantities and take only the real part at the end of a calculation.

I agree with the first sentence, because it says voltage and current are represented as complex quantities. This is similar to what I wrote previously about impedance. Removing represented would be, in my view, a mistake.

Now, as I read it, the antecedent for the word these in the second sentence is complex quantities. I expect most readers will read the real part (mentioned next) of a complex quantity as its real component. That real part, as I said before, is neither magnitude nor phase, though these are both real as well. All the best, gaussmarkov 07:21, 6 September 2007 (UTC)

"The proportionality constants between the complex amplitudes of the voltage and the current in an inductor or capacitor play a similar role to that of the resistance in a resistor. These quantities are called the impedances (of which resistance is a subclass)" (Su, Kendall, 1978, Fundamentals of Circuits, Electronics, and Signal Analysis).

Since this article is about electrical impedance, it follows that EE textbooks (such as the one I cite above) and EE reference books are authoritative references here and not technical level electronics and physics textbooks.

As to your second point, please note that the section in question gives the voltage and current as complex valued functions of time. These are not phasors! Phasors are discussed after this section you give above. Don't forget, the use of phasors to solve AC circuits is, as I have stated before on this talk page, in fact justified by representing (pretending) that the voltages and currents in the circuit are complex valued functions of time, solving, and then taking the real part at the end. Then, we find that we only need to keep up with the complex amplitude (the phasors) of the complex valued time functions while solving the circuit. But, at the end, if we want the actual time varying functions back, we must first multiply the phasor solution by $e^{j\omega _{0}t}$ (giving us back the complex valued time function) and then take the real part of that to get the actual real valued time dependent voltage or current.

Based on your question about this, I have changed "complex quantity" to "complex valued functions of time" Alfred Centauri 14:51, 6 September 2007 (UTC)

BTW, in this textbook which I have taught from, the terms complex impedance and impedance are used interchangeably. That is, impedance is not used to mean the magnitude of the complex impedance in this textbook. —Preceding unsigned comment added by Alfred Centauri (talk • contribs) 15:15, 6 September 2007 (UTC)

Indeed, I confused phasors with voltage and current as functions of time. Thank you for straightening me out.

I spent some time in the Engineering Library this morning and found some books that described impedance in noncomplex ways. See for example, Jones, Laughton, & Say, Electrical Engineer's Reference Book. As I read him, Hambly (which you mention) clearly starts with complex impedance and then shortens it to impedance. I was surprised to read that you view EE textbooks as the only authorities. At the bottom of this page this article is classified under Physics articles with comments | Unassessed physics articles. Perhaps we could apply the WP:NPOV and broaden the range of authorities? It did not occur to me that electrical implied EE and I am confident that a lot of readers are not coming from or looking for an EE treatment.

I made a few edits that I hope are at least constructive, if not acceptable. Cheers, gaussmarkov 22:21, 6 June 2007 (UTC)

BTW, I meant to add that the majority of EE textbooks that I examined certainly talk exclusively about impedance as complex. I want to acknowledge this. In my rewording of the introductory paragraph, I replace the phrase "in general" with "often" to reflect this. Perhaps I should have used "usually" -- this seems reasonable also if others prefer it. All the best, gaussmarkov 22:32, 6 June 2007 (UTC)

"Perhaps we could apply the WP:NPOV and broaden the range of authorities?" I don't follow you. If, for example, someone adds something here from a reference of the level of, e.g., "Electronics for Dummies" which clearly contradicts or distorts (for the sake of simplicity) the information in one or more widely cited EE textbooks or reference books, removing that material is not even remotely a POV issue. FWIW, I encourage and have in fact advocated for technical level treatment, e.g., non-complex treatment of impedance in electrical/electronics articles as long as it is not misleading or outright incorrect. Also, keep in mind that many EE students do in fact refer to Wikipedia so, IMHO, it is essential that EE level material is included in these articles. Cheers, Alfred Centauri 22:29, 6 September 2007 (UTC)

I had in mind your exclusion: "EE reference books are authoritative references here and not technical level electronics and physics textbooks." I think it is reasonable to include the electronics and physics textbooks as authoritative in an article on electrical impedance. -- gaussmarkov 05:44, 7 June 2007 (UTC)

"it is reasonable to include the electronics and physics textbooks as authoritative in an article on electrical impedance". Of course it's reasonable and I don't think that I said that they should be excluded. I think you've misintepreted what I meant. There is a hiearchy of authority when it comes to reference materials, right? So, if an editor puts in material that is questionable and supports it with a reference whose intended audience is the layperson, technician, or non-EE and then another editor removes or corrects the material and supports the edit with a widely used EE reference, which reference is authoritative in this case? —Preceding unsigned comment added by Alfred Centauri (talk • contribs) 12:54, 7 September 2007 (UTC)

Sorry to break into this discussion like this, but I thought I would take it upon myself to improve the section in question by expanding upon the idea of "taking the real part" with a more-detailed description of why this works. Please pare it down if I've gone overboard here! Oli Filth 15:14, 8 September 2007 (UTC)

Etymology section

While I am sympathetic with the point made in the edit summary associated with the addition of this section ("who came up with the term doesn't need to be in the first sentence"); the creation of a full section seems like overkill unless there are other points of interest in the etymology of the word impedance. A mention of Oliver Heavyside does not need to be in the first sentence, but given his importance in the development of this and related concepts, I feel he is worthy of a mention and the opening section is probably the best place for it. I will revert shortly unless there are good arguments made for keeping it, or suggestions for additional etymological content.--DJIndica 21:56, 12 September 2007 (UTC)

Yes, a new section is probably overkill, but can you try something different like making it the second sentence. No need to state everything in one sentence. —Pengo 02:42, 13 September 2007 (UTC)

WikiProject Electronics quality and importance assessment

It has been noted by a number of contributors that this page can vary significantly in quality over time due to the large number of edits, some of which are ill informed and detract from the information content and/or readability, and can add false or misleading information. It seems to me that it would be a good idea to rate the quality and importance of the article using the WikiProject Electronics scales.

My thinking is that this will in the first instance hopefully put it on the radar of more people with genuine knowledge and interest in this area. In the long run, if the article reaches the point where it is assessed as a good article then it may encourage more thoughtful edits in the future. I have added the banner at the top of this page and taken the liberty of adding a 'high importance' tag; I don't think it is controversial to state that impedance is an important topic in electronics.

It would be good to see comments here, suggesting people's thoughts on the current quality of the article along with suggestions for improvements, perhaps based on good and featured articles on related topics.--DJIndica 23:02, 19 October 2007 (UTC)

Electromagnetism template

This article is one of only a couple of those listed in the electromagnetism template that does not include the template. There are definitely arguments against including it (not least that it is rather long and would require moving the images around), but I think it is probably worth having. I have tried playing around with the positioning of the first image in combination with the template; an example of one possibe arrangement can be found here. --DJIndica 16:57, 22 October 2007 (UTC)

Merger proposal

It is proposed to merge Impedance of different devices (derivations) into this article. The article says little or nothing that is not already said here and said better and in places is just plain wrong. Besides which it is practically orphaned. SpinningSpark 18:42, 14 June 2008 (UTC)

I have created a version of this article including the derivations at User:DJIndica/Sandbox2. I'd appreciate any comments.--DJIndica (talk) 12:29, 18 July 2008 (UTC)

Question

Vp stands for peak voltage, right? I'm referring to the part about capacitors in the Device Examples section of the article. If not please explicitly state what Vp is, since I don't think it is something that can be easily inferred from the article. 96.60.80.133 (talk) 03:09, 13 November 2008 (UTC)

I would also like to add that I found this article very helpful. From reading some of the discussion here I understand that some of you guys are extremely intelligent and I thank you for all your contributions. 96.60.80.133 (talk) 03:38, 13 November 2008 (UTC)

V_p is the voltage amplitude, which is indeed the peak voltage given that there is no DC offset.--DJIndica (talk) 19:01, 13 November 2008 (UTC)

Archive 1

Archive 2

Archive 3